Calculating The Properties of Intersecting Cones

Table of Contents

Introduction

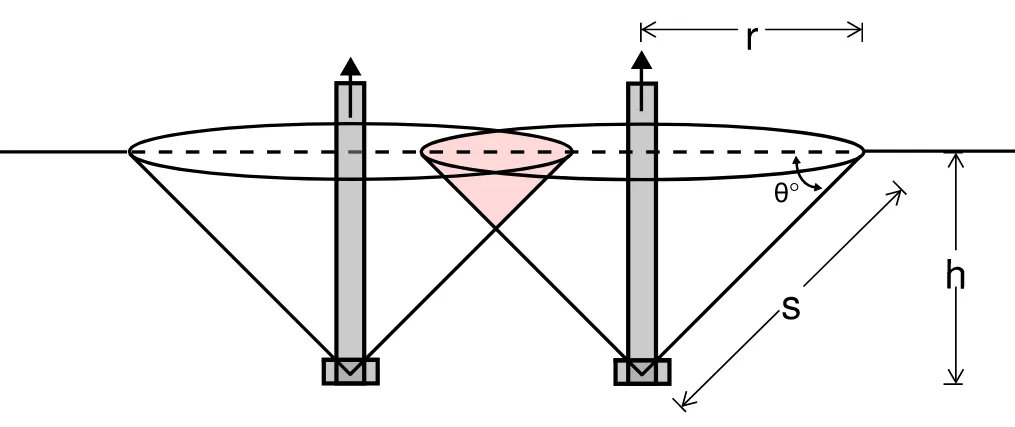
In anchor design the cone is the idealised shape used to represent the failure surface for pullout calculations.

For something like an anchor in concrete we can use the strength of the concrete along the surface area of the cone to resist the breakout force. For a rock anchor however due to defects in the rock we may not by able to rely on the unit as if it is a single homogenous piece. In this case, to resist pullout we can however rely on the deadweight of the cone.

As such calculating the surface area and volume of cones can be important for engineering design. However, when we have multiple anchors in close proximity the cones will intersect and the volume (and surface area) of the intersecting cones will need to be calculated.

Over the years I have developed methods to help calculate the volume of intersecting cones. This post will outline the methods I have developed.

Volume of a Single Cone

The calculation for the volume of a cone is well known, and relevant to the design of a single anchor. The formula for the volume of a cone is:

$V = \frac{1}{3} \pi r^2 h$

where:

• ( V ) is the volume of the cone
• ( r ) is the radius of the base of the cone
• ( h ) is the height of the cone

Surface Area of a Single Cone

We may also be interested in the surface area of the cone:

$SA = \pi r^2 + \pi r s$

where:

• ( $π r^2$ ) is the area of the end of the cone
• ( $s$ ) is the slant height of the cone which can be found by $\sqrt{r^2 + h^2}$
• ( $π r s$) is the surface area of the cone excluding the end

Properties of Intersecting Cones

Method 1: Analytical Solution

The analytical solution is of course accurate but also extremely limited in its application.

I have only been able to develop a formula for the intersection of cones with the same height and the same angle of inclination.

I have used this research paper by Harish Chandra Rajpoot of the Indian Institute of Technology Bombay.

In the paper Rajpoot derives a formula for the volume of the minor cone section which is the volume of the cone that is cut off by the intersecting plane. If we had two cones intersecting each other then by adding the major volume of each cone we could get the total volume of the intersecting cones.

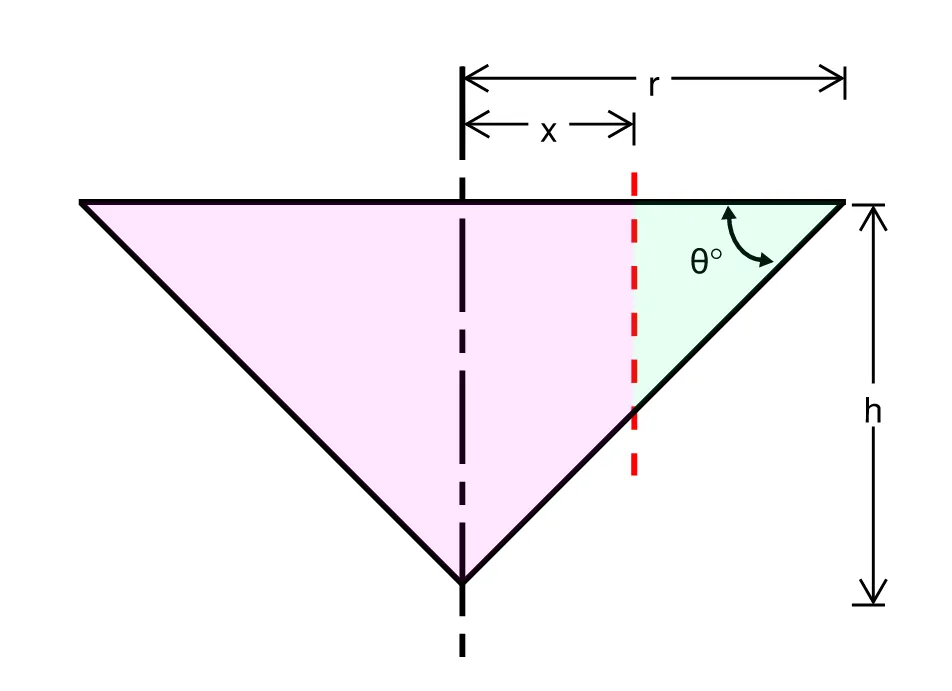
The formula is:

$V_{minor} = \frac{h}{3 \times r} [r^3 \times cos^{-1}(\frac{x}{r})) - 2 \times r \times x \times \sqrt{r^2 - h^2} + x^3 \times ln(\frac{r + \sqrt{r^2 - x^2}}{x})]$

We can then easily deterimine the volume of the major cone section by subtracting the volume of the minor cone section from the volume of the original cone:

$V_{major} = \frac{1}{3} \pi r^2 h - V_{minor}$

Finally if we had two intersecting cones intersecting at the plane then the total volume of the intersecting cones would be:

$V_{total} = 2 \times V_{major}$

Method 2: CAD Solution

Using CAD provides us a solution which is simple, flexible and easy to visually validate. The main drawbacks are needing to create a model which can be slightly time consuming however since most applications simply have a grid of anchors it can be quite easy to work out the volume of the intersecting cones.

I use BricsCAD Shape a free tool which can be used to create 3D CAD models.

Once inside the program I go to Model -> 3D solids -> Cone. Once cone is selected I press anywhere to start drawing the cone. I then type the radius i want and press enter, type the height I want and press enter. I then press enter again to finish the cone.

We now have a single cone.

I then generally can simply copy the cone since i am often trying to model a grid of anchors that are all at the same embedment. I select the cone, type copy and press enter to go to the copy tool and draw the cone to be moving in the plane i am after before i type the spacing i want and press enter.

We now have two overlapping, but single cones.

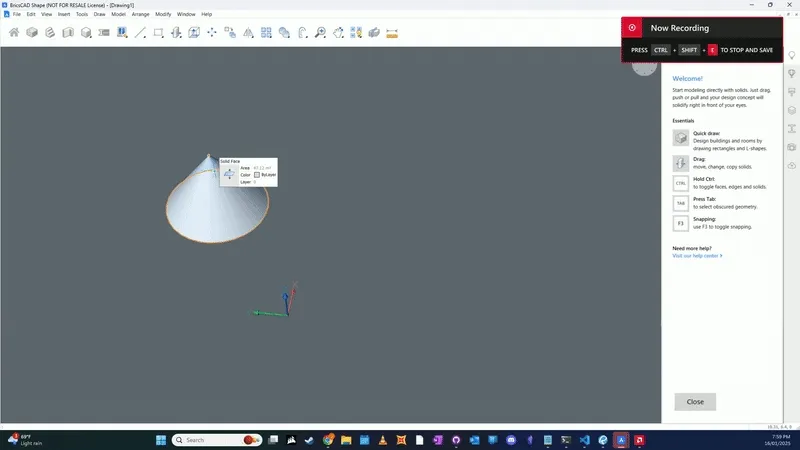
Finally i select both cones and then use the union tool to merge them together.

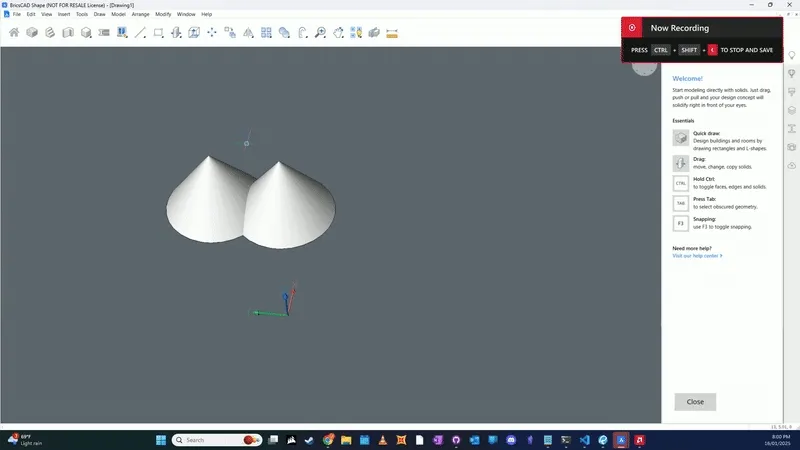
In BricsCAD shape we can see the surface area of the shape, but not the volume. To view the volume of the shape I save the file and open it in Autodesk DWG Trueview and use the “Region/Mass Properties” tool to get the volume.

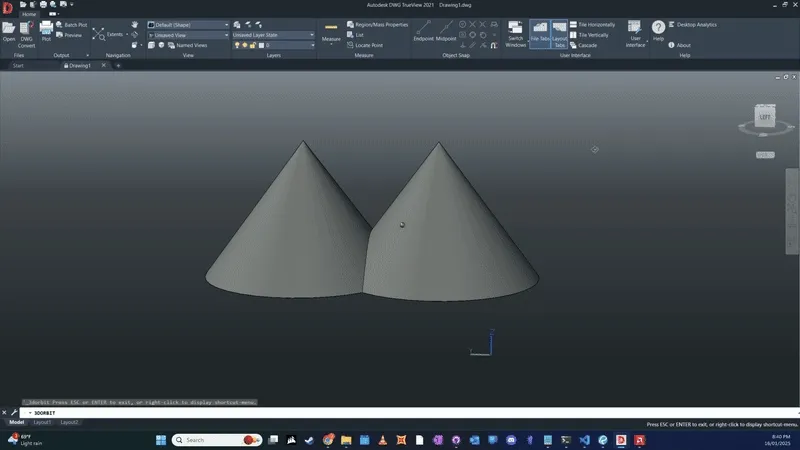
The real benefit of this solution is that is completely flexible so if there is any reason we want to change the geometry of the cone shaped resistance volume we can do so easily. We can also be confident that what we are calculating is a true physical representation of what we intend to model, with a pure mathematical approach it can be hard to visualise what the numbers actually reference if there are many components in our calculation. We can also get the volume and the surface area of the shape.

We could also use this approach to get the surface area and volume for any other type of 3D geometry.

Concluding Remarks

Using the above approach we can get the volume and surface area for a group of intersecting cones. We should be cautious however that we use these values appropriately and check all possible failure mechanisms that can occur. It should also be noted that using the volume of the intersecting cones gives us a lower bound on the volume however the surface area could be smaller if we grouped the cones with one smooth linear surface around the cone group. We should therefore be sure that in applications were we do use the surface area we find the critical surface area for any shape that can CONTAIN the failure cones.

In this example we could also see the power and flexibilty in adapting computer technology to our needs over the development of new mathematical relations.